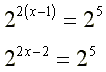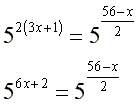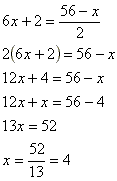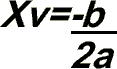um exemplo de logaritmo: todo mundo sabe que 5 elevado à potência 2, resulta 25, correto?
5² = 25.
então complicando um pouquinho, usando log fica assim:
Mas especificamente falando, logarítmos são essenciais para resolver exponenciações mais complicadas como 37 = x.
A resposta fica : X = log 3 7 = 1,771243749
Definição.
Logaritmo de um número n na base b, é o n° x, ao qual devemos elevar a base b para obtermos o n.
sendo assim, indicamos : log b n = x <=> bx = n
chamamos : n: logaritmando
b: base
x: logaritmo.
exemplo numérico: log 3 9 = 2 <=> 32 = 9 = 9 = logaritmando
3 = base
2 = logaritmo
Condições de existência
Existem algumas regras para que os logaritmos sejam escritos.
1° Logaritmando deve ser um número positivo.
2° a base deve ser um n° positivo diferente de 1.
a base não pode ser 0.
TRADUZINDO: existe log b n quando b > 0, b ≠ 1 e n > 0
exemplo:
Para que valores de X existe log 3 (5x – 10) ?
5x - 10 > 0
5x > 10
x > 10 / 5 = x > 2
R: { x € R | x > 2 } .
pronto.